Java Applet on Generalized Additive Decomposition

Java Applet on Generalized Additive Decomposition

Start the applet

INTRODUCTION

Applet enables to decompose prototype machine with distribution of micro-operations among sub-machines (corresponding to the given cover on the set of micro-operations) that is not possible to achieve using alternative approach. To construct such network we apply the method of decomposition that proceeds from a given cover (not a partition) on the set of states of prototype FSM. Here we can consider the decomposition technique for controller and data-path simultaneously and develop a decomposition procedure for the finite state machines with data-path model.

SHORT THEORETICAL BASICS

Prototype FSM model

Formally, FSM is a quintuple < S, X, Y, , > where

S = { s1, … , sn } is a set of states;

X = { x1, … , xl } is a set of primary input variables;

Y = { y1, … , ym } is a set of primary output variables;

: D() S is a multiple valued next state function with
domain D () ={0, 1} l S and codomain S ;
{0, 1} represents a set of values (symbols) each input variable xi may assume;

: D() R() is an output function with
domain D() = {0, 1} l S and codomain R() ={0, 1}m ;
{0, 1} is a set of values each output variable yi may assume.

Finite state machine with data-path (FSMD)

An FSMD is formulated as a quintuple:

< S, I SS, O AS, , >

S is the set of states of the FSMD
I SS is the set of inputs of the FSMD. Inputs extended with status expressions
O AS is the set of outputs of the FSMD. Outputs extended with variable assignments

is the next state function, mapping
S (I SS) S
is the output function, mapping
S (I SS) (O AS)

Example Prototype FSM

S= { s1 , s2 , … , s8 }

X= { x1, x2 , … , x8 }

Y= { y1 , y2 , … , y14 }

Decomposition procedures

Generation of the initial partition
Definition of states in component FSMs
Definition of the set of external input variables of component FSM
Generation of the set of the set of internal (additional) input variables
Definition of the set of output variables of component FSMs
Generation of transition and output functions of component FSMs
Realization of FSM network.

The set of states of (component) sub-FSM

= {Y1, … Yn} is the partition on the set of output variables Y.

G = {g1, … gH} is the set of g-transitions in the transition table

X(gh) and Y(gh) are the sets of essential input and output variables (microoperations) in the g-transition gh(h = 1, … H),

X(si) and Y(si) are the sets of input and output variables at the transitions from the state si.

Set of external input variables

Initial partition on Y:
= { {y1, y3, y4, y7}, {y6, y8, y9 }, {y2, y5, y10}

Induced cover on S:
={ {s1, s4, s7}, {s4, s5, s8}, {s2, s3, s6} }

Induced cover on G:
={ {1, 2, 7, 8, 17}, {9, 10, 11, 12, 13, 18, 19}, {3, 4, 5, 6, 4,15,16} }

Decomposition procedure

Let us put the network N with n component FSM
Ap = < Sp, Xp, Vp, p, p >, p = 1, … n,

in accordance to triplet < A, , , >.

The number of component machines is equal to the number of blocks in the partition (or the cover and ).

Sp = Bp {bp} is the set of states in the component controller Cp,
where Bp is the p-th block of the cover , and bp is additional state in Cp.

Xp = X(Gp) Zxp is the set of input variables in the component controller Cp.

X(gh) is the set of essential input variables in the g-transition gh of the controller C of the prototype FSM;
Gp is the p-th block of the cover .
Zxp = {zt / (sj , h) = st ; st Sp , sj Sp}.
Vp = Yp Zyp
Zyp = {zi / (st , h) = sj ; st Sp , sj Sk, st Sk}.
Assume that there is a g-transition in of prototype FSM
< sj, st, h, h >
(the transition from sj to st with the input condition h and the output h in the controller C):
(sj , h) = st; (sj , h) = h
Define the corresponding transitions in component controller.
j be the set of component controllers with the state sj,

t be the set of component controllers with the state st,

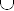
jt = j t be the set of component controllers with the states sj and st
If Ck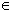 jt , then in Ck k(sj , h) = st.

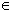
If Ap j \ jt, then in Cp p(sj , h) = bp,
(si is the state of Cp and st is not the state of Cp)

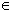
The output controlling datapath of qth sub-FSMD for controller Cq j
is equal to h Yq
(si is the state of Cq and it is also possible that the next state st is the state of Cq).

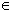
In addition to controlling outputs, one and only one controller from j (say Cr), must generate the output signal which forces each controller from Cu t \ jt (if this set is not empty) to transit from the additional (idle) state bu to st and in Cq
r (sj, h) = h Yu {zt}.

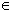
If Cu t \ jt (st is the state of Cu and sj is not the state of Cu), then in Cu
u(bu , zt) = st
u (bu, zt) = Y0

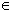
The initial state of the component controller is equal to s0 , if Cp 1 and bp otherwise.

Components transition tables

The set of states of the first component is the states from the first block of cover plus b1, S1 = {s1, s4, s7, b1}.
The set of outputs consists of variables from Y which are in g-transitions from the first block of cover plus additional output variable z3 because there is transition from s4 to s3 in the original transition table, but s3 is the state of the second component C2.

The set of inputs consists of variables which are in g-transitions from the first block of cover plus additional input variable z4 because exists g-transition (11) not included in the first block of cover with next state s4.

The first component transition table

The second component transition table

The third component transition table

Transitions between sub-machines

Note, that 4 = { C1, C2 } and 3 = { C3 }, but only C1 generates output z3.

Note, that when there is transition to the state s4 both controllers C1 and C2 are activated but only one of them will generate outputs controlling own data-path.

The data-path of other machine will be silent (it depends on the value of input variable x1).

FSMD network

Additional theory is available here or here

APPLET MANUAL

LIST OF PUBLICATIONS:

WARNING: This page contains links to PDF files of articles that may be covered by copyright. You may browse the articles at your convenience. (in the same spirit as you may read a journal or a proceeding article in a public library). Retrieving, copying, or distributing these files, however, may violate the copyright protection law. We recommend that the user abides international law in accessing this directory.

A. Sudnitson, “Fininite State Machines with Datapath Partitioning for Low Power Synthesis”, in Proc. 8th International Conference Mixed Design of Integrated Circuits and Systems ( MIXDES’2001), Zakopane, Poland, 2001, pp.163-168. (ISBN: 83-87202-98-3)

S. Devadze, E. Fomina, M. Kruus, and A. Sudnitson, “Web-Based System for Sequential Machines Decomposition”, in Proc. IEEE EUROCON 2003 International Conference on Computer as a Tool, Ljubljana, Slovenia, 2003, V. 1, pp. 57-61. (ISBN: 0-7803-7763-X, IEEE Catalog No.: 03EX665)

A. Jutman, A. Sudnitson, and R. Ubar, “Digital Design Learning System Based on Java Applets”, in Proc. 4th Annual Conference of the LTSN Centre for Information and Computer Sciences, NUI Galway, Ireland, 2003, pp.183-187. (ISBN: 0-9541927-4-5)