Topics: Fault Modeling and Simulation

FAULT MODELING AND SIMULATION

1.1. Logical fault models
 

Logical faults represent the effect of physical faults on the behavior of the system.
Why we model physical faults as logical ones:

• complexity of simulation reduces (many physical faults may be modeled by the same logical fault);
• one logical fault model is applicable to many technologies;
• logical fault tests may be used for physical faults whose effect is not completely understood.

• explicit faults may be enumerated;
• implicit faults are given by some characterizing properties.

• structural faults are related to structural models, they modify interconnections between components;
• functional faults are related to functional models, they modify functions of components.

Structural fault models assume that components are fault-free and only their interconnections are affected:

• a short is formed by connecting points not intended to be connected;
• an open results from the breaking of a connection.

• a line l is stuck at a fixed logic value v (v {0,1}), denoted by l/v;

• a short between ground (s-a-0) or power (s-a-1) and a signal line;
• an open on a unidirectional signal line;
• any internal fault in the component driving its output that it keeps a constant value;

 

• bridging faults (shorts between signal lines) with two types: AND and OR bridging faults (depending on the technology).

1.2. Fault Detection and Redundancy

1.2.1. Fault detection in combinational circuits
1.2.2. Detectability of faults
1.2.3. Redundancy

1.2.1. Fault Detection in Combinational Circuits

Circuit: Let Z(x) be the logic function of a circuit N, where x represents an arbitrary input vector and Z(x) denotes the mapping realized by N.

Faulty circuit: The presence of a fault f transforms N into a new circuit N_f with a new function Z_f (x).

Test: Denote by t a specific input vector (test vector), and by Z(t) the response of N. Let us call a sequence of test vectors by test:
T={t₁ t₂ ... t_n }.

The circuit is tested by applying a test T and by comparing the output response with the expected output response of N, .

Fault detection: A test vector t detects a fault f iff.

Fault sensitization: A line in a circuit whose value in the test t changes in the presence of the fault f is said to be sensitized to the fault f by the test t. We say also: the test t activates a fault f. A path composed of sensitized lines is called a sensitized path.
We say also: the test t propagates a fault (fault effect) along sensitized path.

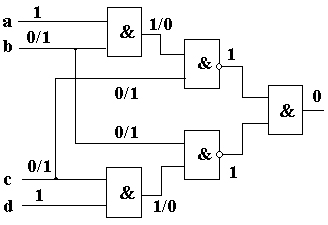
Example:

1. In Figure a fault a/0 is sensitized by the value 1 on a line a.

2. A test t = 1101 is simulated, both without and with the fault a/0. The results of the simulation are different in the two cases, shown in a form  where  and  are corresponding signal values in the fault-free and in the faulty circuit. The fault is detected since the output values in the two cases are different. A path from the faulty line a is sensitized (bold lines) to the primary output of the circuit.

1.2.2. Detectability of Faults

A fault f is detectable if there exists a test t that detects f , otherwise, f is an undetectable fault.

For an undetectable fault f , , and no test can simultaneously activate f and create a sensitized path to a primary output.

Note: The presence of an undetectable fault f may prevent the detection of another fault g , even then when there exists a test which detects the fault g.

Example: In Figure, the fault b/1 is undetectable. As we saw in the previous example, the test t = 1101 detects the fault a/0. However, in the presents of b/1, the test t is not any more able to detect the fault a/0.

1.2.3. Redundancy

A combinational circuit that contains an undetectable stuck fault is said to be redundant, since such a circuit can always be simplified by removing at least one gate or gate input:

• Suppose that a s-a-1 fault on an input of an AND gate is undetectable. Since the function of the gate does not change in the presence of the fault, we can permanently place a 1 value on that input. But an n-input AND with a constant 1 value on one input is logically equivalent to the (n-1)-input AND obtained by removing the gate input with the constant signal.
• Similarly, if an AND input s-a-0 is undetectable, the AND gate can be removed and replaced by a 0 signal.

A combinational circuit in which all stuck faults are detectable is said to be irredundant.

Redundancy may be introduced on purpose in the following cases:

• in designing fault-tolerant or self-testing circuits,
• in designing circuits to avoid hazards

 

1.3.1. Fault equivalence classes
1.3.2. Equivalence fault collapsing
1.3.3. Fault location
 
 

1.3.1. Fault Equivalence Classes

Two faults f and g are said to be functionally equivalent iff .

A test t is said to distinguish between two faults f and g if ; such faults are distinguishable. There is no test that can distinguish between two functionally equivalent faults.

The relation of functional equivalence partitions the set of all possible faults into functional equivalence classes. For fault analysis it is sufficient to consider only one representative fault from every equivalence class.
   

1.3.2. Equivalence Fault Collapsing

With any n-input gate we can associate 2(n + 1) single stuck faults. For a NAND gate all the input s-a-0 faults and the output s-a-1 are functionally equivalent.

In general, for a gate with controlling value c and inversion i , all the input s-a-c faults and the output  are functionally equivalent. Thus for an n-input gate (n>1) we need to consider only n+2 single stuck faults.

This type of reduction of the set of faults to be analyzed based on equivalence relations is called equivalence fault collapsing.
   

1.3.3. Fault Location

If in addition to fault detection, the goal of testing is fault location as well, we need to apply a test that not only detects the detectable faults but also distinguishes among them as much as possible. A complete location test distinguishes between every pair of distinguishable faults in a circuit.

The presence of an undetectable fault may invalidate a complete location test. If f and g are two distinguishable faults, they may become functionally equivalent in the presence of an undetectable fault.

A complete location test can diagnose a fault to within a functional equivalence class. This is the maximal diagnostic resolution that can be achieved.

Two faults f and g are functionally equivalent under a test T iff  for every test vector .

Functional equivalence implies equivalence under any test but equivalence under a given test does not imply functional equivalence.

1.4. Fault Dominance

If the objective of a testing is limited to fault detection only, then in addition to fault equivalence, another fault relation can be used to reduce the number of faults that must be considered.

Definition. Let T_g be the set of all test vectors that detect a fault g. A fault f dominates the fault g iff f and g are functionally equivalent under T_g.

If f dominates g , then any test t that detects g will also detect f. Therefore, for fault detection it is unnecessary to consider the dominating fault f , since by deriving a test for g we automatically obtain a test that detects f as well.

1.5. Single Stuck-Fault Model

Single stuck-fault model (SSF) is the classical or standard fault model. Its usefulness results from the following attributes:

• it presents many different physical faults;
• it is independent of technology;
• experience has shown that test that detect SSFs detect many non-classical faults as well;
• compared to other fault models, the number of SSFs in a circuit is small;
• SSFs can be used to model other type of faults.

1.6.1. The number of multiple faults
1.6.2. Fault masking
1.6.3. Circular fault masking

1.6.1. The Number of Multiple Faults

Multiple stuck-fault (MSF) model is a straightforward extension of the SSF model in which several lines can be simultaneously stuck.

If n - is the number of possible SSF sites, there are 2n possible SSFs, but there are possible MSFs.

If we assume that the multiplicity of faults is no greater than k , then the number of possible MSFs is

The number of multiple faults is very big. However, their consideration is needed because of possible fault masking.

1.6.2. Fault Masking

Definition. Let T_g be the test that detects a fault g . We say that a fault f functionally masks the fault g iff the multiple fault { f, g } is not detected by any test in T_g .

Example: In Figure the test 011 is the only test that detects the fault c/0. The same test does not detect the multiple fault { c/0, a/1}. Thus a/1 masks c/0.

Definition. Let be the set of all tests in T that detect a fault g. A fault f masks the fault g under a test T iff the multiple fault { f , g } is not detected by any test in T_g’.

Functional masking implies masking under any test, but the converse statement is not always true.

1.6.3. Circular Fault Masking

Multiple fault F may be not detected by a complete test T for single faults because of circular masking relations under T among the components of F.

Example: The test T = {1111, 0111, 1110, 1001, 1010, 0101} detects every SSF in the circuit in Figure. Let f be b/1 and g be c/1. The only test in T that detects the single faults f and g is 1001. However, the multiple fault { f , g } is not detected because under the test vector 1001, f masks g and g masks f .