Topic: Algebra

1. ALGEBRA
   

1.1. Relations

Def A relation between a set S and a set T is a subset R of ST; and for (s,t) in R we write s R t. Thus R={(s,t)|s R t}.

A relation R on SS (sometimes called simply a relation on S) is:

• reflexive if, for all s, s R s;
• symmetric if s R t implies t R s;
• transitive if s R t and t R u implies s R u.

1.2. Partitions

1.2.1. Definition of partitions

Def A partition on S is a collection of disjoint subsets of S whose set union is S, i.e.  such that and 

The partition is the measure of information.

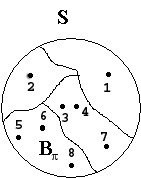
We refer to the sets of  as blocks of  and designate the block which contains s by .

1.2.2. Sample partition
 
 

1.2.3. Operations with partitions

If s and t are in the same block of , we write:

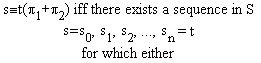
The computation of 
The computation of  : to compute  we proceed inductively. Let

and for i>1 let

Then

for any i such that .
and 

For  and on S we say that  is larger than or equal to  and write  if and only if every block of  is contained in a block of . Thus  if and only if and if and only if .

Operations "·" , "+" and the ordering of partitions form the basic link between machine concepts and algebra.